NP-Completeness

NP-completeness is an important advance in the question of P vs NP

Some problems can be formally linked to the rest of $\text{NP}$, meaning a solution to these problems implies a solution to the rest of $\text{NP}$

This is very important practically, because it means we have a means of proving a problem is probably unsolvable in polynomial time

The theory of NP-completeness starts with the satisfiability problem

A Boolean formula is an expression involving Boolean variables and operations, and is satisfiable if some assignment of variables makes the formula evaluate to $1$

$SAT=\{⟨\varphi ⟩\mid \varphi \text{ is a satisfiable Boolean formula}\}$

Theorem: $SAT\in \text{P}$ $⟺$ $\text{P}=\text{NP}$

How is this true? We use the concept of reducibility to prove this theorem

Definition: A function $f:{\Sigma }^{\ast }\to {\Sigma }^{\ast }$ is a polynomial time computable function if some polynomial time Turing machine $M$ exists that halts with just $f(w)$ on its tape, when started on any input $w$

Definition: Language $A$ is polynomial time (mapping) reducible to language $B$, written $A{\le }_{p}B$ if a polynomial time computable function $f$ exists, where $w\in A⟺f(w)\in B$

We call $f$ a polynomial time reduction

This is an analog to mapping reducibility, and it’s useful because it establishes shortcuts for proving membership to $\text{P}$, and therefore $\text{NP}$

Theorem: If $A{\le }_{p}B$ and $B\in P$, then $A\in P$

As an example, we first introduce a slight variation on the satisfiability problem

A literal is a Boolean variable or a negated Boolean variable, a clause is several literals connected with $\vee$s, and a Boolean formula is in conjunctive normal form (called a cnf-formula) if it comprises of clauses connected with $\wedge$s

A cnf-formula is called a 3cnf-formula if all clauses have three literals
$3SAT=\{⟨\varphi ⟩\mid \varphi \text{ is a satisfiable 3cnf-formula}\}$

Theorem: $3SAT{\le }_{p}CLIQUE$

We convert a 3cnf-formula into a clique problem by creating a node for each item in all $k$ clauses and making an edge two nodes if they are in different clauses and are not negations of each other; then, we test for a $k$-clique

This tells us that if $CLIQUE$ is solvable in polynomial time then so is $3SAT$, even though they are quite different looking problems

Definition: A language $B$ is NP-complete if $B$ is in $\text{NP}$ and every $A$ in $\text{NP}$ is polynomial time reducible to $B$

If $B$ is $\text{NP}$-complete and $B\in P$, then $\text{P}=\text{NP}$
If $B$ is $\text{NP}$-complete and $B{\le }_{p}C$ for $C$ in $\text{NP}$, then $C$ is $\text{NP}$-complete

This is fascinating, but requires us to have a single $\text{NP}$-complete problem before we can connect other problems

Theorem: $SAT$ is $\text{NP}$-complete

This is not a simple proof, since it requires showing that any language in $\text{NP}$ is polynomial time reducible to $SAT$, a fact that looks ridiculous at first glance (at least to me), but makes more sense when you consider that Boolean operations are the basis for electronic circuitry

The reduction is fairly simple conceptually but requires dealing with many details

Proof:
To start, $SAT$ is trivially in $\text{NP}$

Let $N$ be a nondeterministic Turing machine that decides $A$ in $n^k$ time
A tableau for $N$ on $w$ is an $n^k\times n^k$ table whose rows are the configurations of a branch of $N$ on $w$

Each row starts and ends with $\#$ and we place the head’s state at its location on the tape, offsetting the rest of the tape (due to this configuration, we technically assume the machine decides $A$ in $n^k-3$)

A tableau is accepting if any row of the tableau is an accepting configuration, so the problem of determining whether $N$ accepts $w$ amounts to determining if an accepting tableau for $N$ on $w$ exists

Let $C=Q\cup \Gamma \cup \{\#\}$, where $Q$ is the state set and $\Gamma$ is the tape alphabet
For each $i,j\in [1,n^k]$ and $s\in C$, we have a variable $x_{i,j,s}$
Each of the $(n^k{)}^2$ entries of the tableau is called a cell, and its value is designated through the variable $x_{i,j,s}$ which takes on the value $1$

Let’s now produce a formula $\varphi$ that corresponds to an accepting tableau for $N$ on $w$, which will take the form $\varphi ={\varphi }_{\text{cell}}\wedge {\varphi }_{\text{start}}\wedge {\varphi }_{\text{move}}\wedge {\varphi }_{\text{accept}}$

We first guarantee that each cell has a single value set, through the expression ${\varphi }_{\text{cell}}=\underset{1\le i,j\le n^k}{\bigwedge }\left[\right(\underset{s\in C}{\bigvee }{x}_{i,j,s})\wedge (\underset{\begin{array}{c}s,t\in C\\ s\ne t\end{array}}{\bigwedge }(\overline{x_{i,j,s}}\vee \overline{x_{i,j,t}})\left)\right]$

Then, we explicitly require the first row to be the starting configuration with ${\varphi }_{\text{start}}=x_{1,1,\#}\wedge x_{1,2,q_0}\wedge x_{1,3,w_1}\wedge \cdots \wedge x_{1,n+2,w_n}\wedge x_{1,n+3,\bigsqcup }\wedge \cdots \wedge x_{1,n^k-1,\bigsqcup }\wedge x_{1,n^k,\#}$

We require an accepting configuration ${\varphi }_{\text{accept}}=\underset{1\le i,j\le n^k}{\bigvee }{x}_{i,j,q_{\text{accept}}}$

Our final formula ${\varphi }_{\text{move}}$ is the most complex, guaranteeing that configurations are legal by scanning through the cells with a $2\times 3$ window, which is enough context to guarantee transitions are valid

If the top row of the tableau is the start configuration and every window in the tableau is legal, then each row of the tableau is a configuration that legally follows the preceding one

We omit the precise definition and write ${\varphi }_{\text{move}}=\underset{1\le i<n^k,1<j<n^k}{\bigwedge }\underset{\begin{array}{c}{a}_1,\dots ,a_6\\ \text{is a legal window}\end{array}}{\bigvee }(x_{i,j-1,a_1}\wedge \cdots \wedge x_{i+1,j+1,a_6})$

”$a_1,\dots ,a_6$ is a legal window” is a well-defined boolean expression dependent on the Turing machine’s transition function

$\varphi$‘s total size is $O(n^{2k})$, which shows we can define $\varphi$ in polynomial time

Thus, we can reduce any Turing machine $N$ on $w$ into a $SAT$ problem, which proves the Cook-Levin theorem, showing $SAT$ is $\text{NP}$-complete

Corollary: $3SAT$ is $\text{NP}$-complete

We note that we can use some Boolean algebra to create $\varphi$ from the $SAT$ proof in 3cnf, by distributing when necessary and splitting larger clauses like $(a_1\vee a_2\vee a_3\vee a_4)$ into $(a_1\vee a_2\vee z)\wedge (\bar{z}\vee a_3\vee a_4)$

NP-Complete Problems

For reasons not well understood, most naturally occurring $\text{NP}$-problems are either in $\text{P}$ or $\text{NP}$-complete

Proving a problem is $\text{NP}$-complete is useful because it tells you a better solution does not exist (for all intents and purposes)

To do this, we look for structures in a language that can simulate the variables and clauses in Boolean formulas, sometimes called gadgets

Our previous theorem now tells us $CLIQUE$ is $\text{NP}$-complete

A vertex cover of an undirected graph $G$ is a subset of the nodes where every edge of $G$ touches one of the nodes

Theorem: $VERTEX$-$COVER=\{⟨G,k⟩\mid G\text{ is an undirected graph that }\text{has a }k\text{-node cover}\}$ is $\text{NP}$-complete

For each variable $x$ in $\varphi$, we produce an edge connecting two nodes, labeled $x$ and $\bar{x}$

For each clause in $\varphi$, we produce a node for each variable in the clause, all connected to each other, and all connected to their corresponding variable node as specified above

$G$ has $2m+3l$ nodes, where $\varphi$ has $m$ variables and $l$ clauses, and we let $k=m+2l$

We create a cover from a solution of $\varphi$ by taking the true literal variables in the cover, and excluding one true literal in each clause triplet

A little thought shows that we can also do the inverse, so $VERTEX$-$COVER$ polynomially reduces to $3SAT$ and is therefore $\text{NP}$-complete

The takeaway in this example is that we are looking to simulate variables and clauses in the problem we’re looking to reduce

Theorem: $HAMPATH$ is $\text{NP}$-complete

We look to show that for any 3cnf-formula $\varphi$, we can construct a directed graph $G$ with two nodes, $s$ and $t$, where a Hamiltonian path exists between $s$ and $t$ $⟺$ $\varphi$ is satisfiable

$\varphi =(a_1\vee b_1\vee c_1)\wedge \cdots \wedge (a_k\vee b_k\vee c_k)$ where each $a,b,c$ is a literal $x_i$ or ${\bar{x}}_i$ for $x_1,\dots ,x_l$

The graph looks like a sequence of diamonds representing each variable, where $s$ starts at the start of the diamond of $x_1$ and ends at the end of the diamond of $x_l$

Each diamond allows for two possible paths that snake through, going from the start to the left represents $x_i$ and going to the right represents ${\bar{x}}_i$

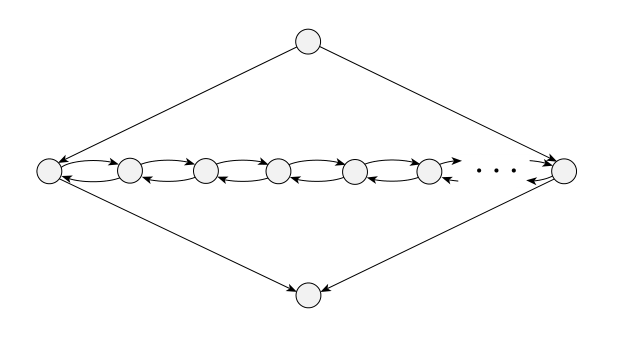
Hence, with this construction, a path encodes a selection of $x_i$ or ${\bar{x}}_i$ for each $i$

Now how do we encode the clauses? The key is that in the center of each diamond we hold $3k+1$ intermediate nodes, corresponding to pairs for each clause and separators between these pairs

To the side of our diamonds, we have one node per clause

These nodes are hooked up to the diamonds such that they can be entered and exited along a path encoding $x_i$ only if the clause contains $x_i$, and they can be entered and exited along a path encoding ${\bar{x}}_i$ only if the clause contains ${\bar{x}}_i$

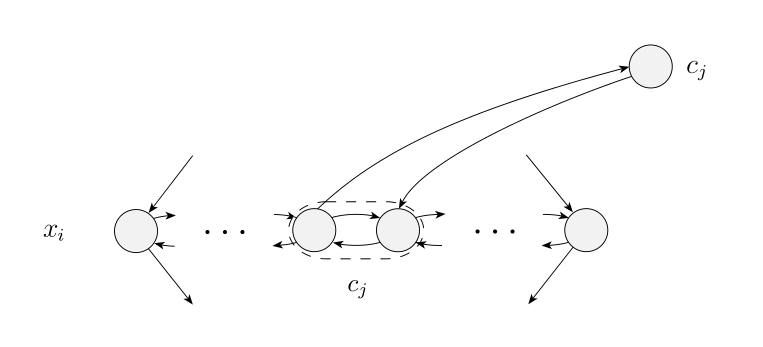
Thus, a satisfiable expression can be converted into a path quite simply, by snaking through the variables according to the selections of $x_i$ and attaching each clause to the path at the first variable that satisfies that clause

The separators in between clause pairs guarantee that any Hamiltonian path must be “normal”, i.e. it follows our expected construction and does not take any shortcuts

Theorem: $UHAMPATH$ is $\text{NP}$-complete

Our construction before no longer works because our connections between a clause and a variable can be satisfied whether a path selects $x_i$ or ${\bar{x}}_i$

Instead, we make a reduction that takes a general directed graph $G$ with nodes $s$ and $t$ and constructs an undirected graph $G^{\prime }$ with nodes $s^{\prime }$ and $t^{\prime }$, such that $G$ has a Hamiltonian path from $s$ to $t$ $⟺$ $G^{\prime }$ has a Hamiltonian path from $s^{\prime }$ to $t^{\prime }$

We replace each node $u$ of $G$ by a triple of nodes $u^{\text{in}},u^{\text{mid}},u^{\text{out}}$ in $G^{\prime }$, except for $s$ and $t$ which are replaced with $s^{\text{out}}=s^{\prime }$ and $t^{\text{in}}=t^{\prime }$ respectively

Then, we add $u^{\text{out}}\leftrightarrow v^{\text{in}}$ in $G^{\prime }$ if $u\to v$ in $G$

It’s clear that a Hamiltonian path in $G$ corresponds to a Hamiltonian path in $G^{\prime }$, if we follow the “intended” directions

And furthermore, the only way to form a Hamiltonian path in $G^{\prime }$ is following the intended direction, because we are forced to hit the middle nodes and therefore must transition from $u^{\text{out}}$ to $v^{\text{in}}$ until we get to $t^{\text{in}}$

Theorem: $SUBSET$-$SUM$ is $\text{NP}$-complete

We reduce $\varphi$ to an instance of $SUBSET$-$SUM$

Each number in the problem has a digit for each variable $x_i$ and a digit for each clause

Each $x_i$ and ${\bar{x}}_i$ transforms to a number with a $1$ in the corresponding digit and a $1$ in each clause that it takes part

In addition, each clause transforms to two identical numbers with a $1$ in the corresponding clause

Then, the problem is to sum to a number with all $1$s in the digit portion and all $3$s in the clause portion