Context-Free Languages

Welp, we’ve proven a lot of languages aren’t regular. Any language that requires counting cannot be regular, since they do not require a constant amount of state.

The class of context-free languages is an intermediate class between the class of regular languages and the class of decidable languages, meaning it is a strict superset of the regular languages

Context-free languages are described by context-free grammars
This class includes N-PDA and the less powerful D-PDA

Instead of writing out a system to recognize languages, we make a system to generate strings inductively. To recognize the language $a^n{b}^n$, we start with a a basis is that $ϵ$ is in the language, and use the recursive step "$w\in A\to awb\in A$".

A grammar is a set of substitution rules for recursively generating strings

Definition: A context-free grammar is a $4$-tuple $(V,\Sigma ,R,S)$, where:

• $V$ is a finite set called the variables
• $\Sigma$ is a finite set, disjoint from $V$, called the terminals
• $R$ is a finite set of rules taking the form $v\to$ a string of variables and terminals
• $S\in V$ is the start symbol

Example: The language $\{a^n{b}^n\}$ for $n\ge 0$
$\{a,b\}$, $\{S\}$, $S$, $S\to aSb\mid ϵ$

We may apply rules recursively however we’d like until all symbols are terminal. This is very powerful.

A derivation of a string is leftmost if we always expand the leftmost variable. Two derivations are different $⟺$ the leftmost (or rightmost) derivation are different.

A parse tree is a tree encoding the steps in a derivation, where leaves are labeled by a terminal or $ϵ$, interior nodes are labeled by a variable, and the root is the start symbol. This is an non-ordered representation of a derivation. We can traverse the leaves with pre-order to get the correct language.

Theorem: For every parse tree, there is a unique leftmost and a unique rightmost derivation

On the topic of ambiguous grammars, Antonella is very amused by “Let’s eat_,_ Grandma”

A grammar is ambiguous if it can yield a string in multiple ways (uniqueness defined as above), or in other words, if there is a string in the language with two different leftmost (or rightmost) derivations. We can make ambiguous grammars for any language, but many have good non-ambiguous grammars. However, some languages are inherently ambiguous (for example, $\{a^i{b}^j{c}^k\mid i=j\text{ or }j=k\}$).

Example:
$S\to S+S\mid S\cdot S$ is ambiguous
$S\to S+s\mid S\cdot s$ is not

In Chomsky Normal Form, every rule takes the form of $A\to BC$ or $A\to a$
To convert a CFG to CNF,

1. Add a new start symbol $S_0\to S$
2. Determine the nullable variables and remove the null transitions
3. Eliminate unit productions
4. Replace long productions with shorter ones
5. Move terminals to unit productions

Swapping steps 4 and 5 works too

What closure properties can we rely on for context-free languages?

1. Union
2. Concatenation
3. Star
4. Intersection
5. Complement

Pushdown Automata

PDAs are equivalent in specification power with CFG, however they recognize a context-free language instead of generating one

They are similar to N-DFA with the addition of a stack

Definition: A pushdown automaton is a 6-tuple ($Q,\Sigma ,\Gamma ,\delta ,q_0,F$), where $Q,\Sigma ,\Gamma ,$ and $F$ are all finite sets, and

1. $Q$ is the set of states,
2. $\Sigma$ is the input alphabet
3. $\Gamma$ is the stack alphabet
4. $\delta :Q\times {\Sigma }_e\times {\Gamma }_e\to \mathcal{P}(Q\times {\Gamma }_e)$ is the transition function,
5. $q_0\in Q$ is the start state, and
6. $F\subseteq Q$ is the set of accept states.

Some CFL are more easily described one way or another

We can also derive relationships between a CFL and RL. For example, $\text{CFL}\cap \text{RL}=\text{CFL}$. To see this, consider crossing a pushdown automata with a DFA.

Theorem: A language is context free $⟺$ some pushdown automaton recognizes it.

It’s not too hard to construct a PDA that mimics a CFG. The other way around is slightly trickier though.

Non-Context-Free Languages

Turns out there are also limitations to context-free languages

There is a pumping lemma on context-free languages, stating that all longer strings can be “pumped”, which in this context means dividing the string into five parts (so that the second and fourth may be repeated together any number of times)

Theorem: If $A$ is a context-free language, $\exists p$ where $\forall s\in A$ such that $|s|\ge p$, $s=uvxyz$ where $\forall i\ge 0$, $u{v}^{i}x{y}^{i}z\in A$, $|vy|>0$, and $|vxy|\le p$

This takes slightly more advanced reasoning than the DFA pumping lemma, but ultimately uses the pigeon-hole principle in a similar way

Deterministic CFL

Deterministic PDAs are actually weaker than the PDAs we’ve examined so far. We still allow the use of $ϵ$ transitions but there can only ever be one valid transition at a time.

Definition: A deterministic pushdown automaton is a 6-tuple,

1. $Q$ is the set of states,
2. $\Sigma$ is the input alphabet,
3. $\Gamma$ is the stack alphabet,
4. $\delta :Q\times {\Sigma }_{ϵ}\times {\Gamma }_{ϵ}\to (Q\times {\Gamma }_{ϵ})\cup \{\varnothing \}$ is the transition function,
5. $q_0\in Q$ is the start state, and
6. $F\subseteq Q$ is the set of accept states.

Exactly one of the states $\delta (q,a,x),\delta (q,a,ϵ),\delta (q,ϵ,x),\delta (q,ϵ,ϵ)$ is not $\varnothing$.

Acceptance occurs as in PDAs. If a DPDA enters an accept state after it has read the last input symbol of an input string, it accepts that string. Rejection occurs if the DPDA doesn’t arrive at an accept state at the end, tries to pop an empty stack (hangs), or makes an endless sequence of $ϵ$-input moves (loops).

Definition: The language of a DPDA is called a deterministic context-free language

To reason more easily about DPDAs, we can first convert any DPDA into one that reads the entire input string.

Theorem: The class of DCFLs is closed under complementation

To see this, we modify a DPDA so that it hits at most one accept state per input symbol (by splitting reading and popping states). Then we invert the reading states.

This theorem implies that some CFLs are not DCFLs. If a CFL’s complement is not a CFL then that CFL is not a DCFL (think $A=\{a^i{b}^j{c}^k\mid i\ne j\text{ or }j\ne k\}$)

DCFLs are not closed under union, intersection, star, and reversal

As a useful tool, we use the fact that $A$ is a DCFL $⟺$ $A⊣$ (with an endmark) is a DCFL

Deterministic pushdown automata are equivalent in power to deterministic context-free grammars, provided we restrict our attention to endmarked languages

Deterministic CFGs are defined in terms of reductions instead of “generations”. If $u$ and $v$ are strings of variables and terminals, we write $u\rightarrowtail v$ to mean $v$ can be obtained from $u$ via a reduce step. $u\stackrel{\ast }{\rightarrowtail }v$ means $v$ can be obtained from $u$ through a series of reduce steps.

In a CFG with start variable $S$ and string $w$, we write a leftmost reduction of $w$ as $w=u_1\rightarrowtail u_2\rightarrowtail \cdots \rightarrowtail u_k=S$. We say that $w$ determines its entire leftmost reduction, which implies the grammar is unambiguous. This is an important but not sufficient requirement.

$xhy\rightarrowtail xTy$ and $T\to h$ means $h$ is a handle of $u_i$

Example: Consider
$R\to S\mid T$
$S\to aSb\mid ab$
$T\to aTbb\mid abb$

This is the language of $\{a^m{b}^m\}\cup \{a^m{b}^{2m}\}$

It should be clear that this is not a DCFL
But if we use $R\to 1S\mid 2T$ then it is

The key idea is we need handles to be restricted so that a DPDA can identify them easily. As in, one must be able to find the handle without knowing the reduce step in advance.

We introduce the requirement that the reduce step is uniquely determined by the prefix of $u_i$ up through and including the reducing string $h$ of that reduce step. In other words, we say that $h$ is a forced handle if $h$ is the unique handle in every valid string $xh{\Sigma }^{\ast }$

Definition: A deterministic context-free grammar is a context-free grammar such that every valid string has a forced handle

For simplicity, we say $S$ isn’t on the right-hand side of any rule, and that there are no unused variables

This is a good definition but doesn’t make it obvious how to determine whether a CFG is deterministic

The DK-test says that for any CFG we can construct an associated DFA $DK$ to identify handles

Each state of the DFA represents our matching progress for each rule. We include transitions for each terminal and symbol. When we reach a symbol, we expand it by each rule.

This test fails,

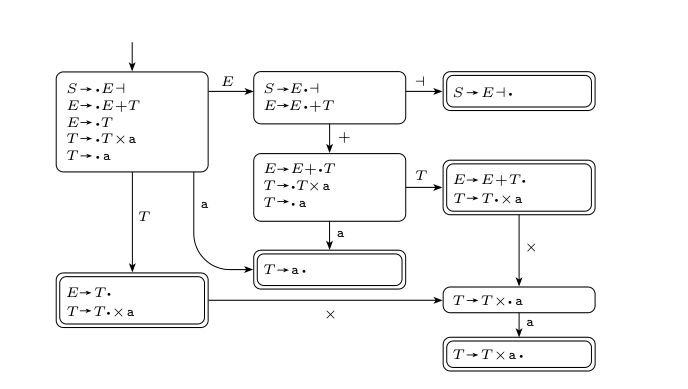
This test passes (note the bottom right box should be $T\to T(T).$),

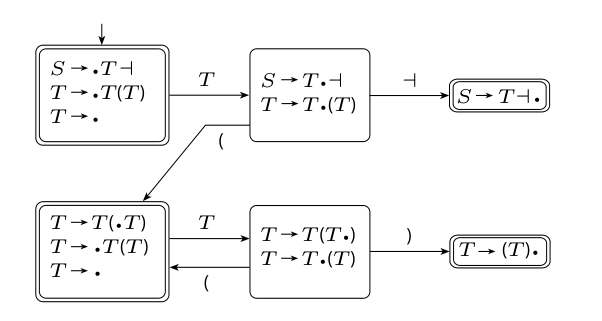
We have a DCFG if each accept state has,

1. Exactly one completed rule
2. No dotted rule in which a terminal symbol immediately follows the dot

Note our definition of a forced handle.

At each step, we run the current string through the machine to end up in a single accept state. If an accept state has multiple rules then we wouldn’t know which one to apply. If an accept state has a terminal symbol transition then we’d be able to move on to another rule, and the result would still be ambiguous. However, if we can transition out of the accept state with a symbol then that previous state is not actually a forced handle, so we safely move on.

Any DCFG can be converted to a DPDA, but only endmarked languages can be converted from a DPDA to a DCFG

Theorem: An endmarked language is generated by a DCFG $⟺$ it is a DCFL

To make a DPDA for a DCFG, we essentially simulate $DK$, keeping its states on the stack, and using that to iteratively reduce any input string. Once we reduce to the start state $S$, we accept.

To do the other way around, is much more complicated and involves the $DK$-test

LR(K) Grammars

DCFGs are great but can be a bit inconvenient with their restrictions

$LR(k)$ grammars are a broader class of grammars, close to DCFGs, that can be directly converted into DPDAs

Definition: In an $LR(k)$ grammar, a handle is forced according to the $k$ symbols following the handle

• Left to right input processing
• Rightmost derivations
• $k$ symbols of lookahead

Therefore, a DCFG is the same as an $LR(0)$ grammar

We can convert any $LR(k)$ grammar to DPDA with a $D{K}_k$ test
A $D{K}_k$ test works quite similar to a $DK$ test, but we keep track of the possible $k$ length strings that could follow a handle after reducing. This lets us track ambiguities in a procedural way.